En indikator, der ofte anvendes i teknisk analyse, som viser den gennemsnitlige værdi af et værdipapir pris over en nærmere fastsat periode. Glidende gennemsnit bruges generelt til at måle fremdriften og definere områder af mulig støtte og modstand.
Glidende gennemsnit kommer i forskellige former, men deres underliggende formål er stadig det samme: at hjælpe tekniske handlende spore udviklingen af finansielle aktiver ved at udjævne de dag-til-dag kursudsving, eller støj.
Forkortelser af de 3 mest anvendte MA
Til information kan det fortælles at der findes flere udgaver af Moving Average (MA). Forneden er de 3 mest anvendte listet:
SMA Simple Moving Average
WMA Weighted Moving Average
EMA Exponential Moving Average
Den væsentligste forskel mellem disse typer af glidende gennemsnit, er vægtningen af de nyeste kurser. SMA bruger en ligelig vægtning af alle de kurser, der indgår i beregningen, mens WMA og EMA vægter de nyeste kurser højest.
Simple Moving Average
Den enkleste form af en glidende gennemsnit, passende kendt som et simpelt glidende gennemsnit (SMA), er beregnet ved at tage det aritmetiske gennemsnit af et bestemt sæt af værdier. For eksempel for, at beregne et grundlæggende 10-dages glidende gennemsnit vil du ligge addere slutkurser fra de sidste 10 dage og derefter dividere resultatet med 10.
WMA – Weighted Moving Average
Weighted Moving Average er et gennemsnit af data, beregnet over en periode, hvor større vægt er knyttet til de seneste data. WMA udglatter en dataserie, hvilket er vigtigt i et volatilt marked, da det hjælper til at identificere tendenser meget lettere. Vægtning beregnes ud fra en sum af dage.
WMA er et vægtet gennemsnit af de sidste n priser, hvor vægtning falder med 1 med hver tidligere pris.
Beregning:
((n * Pn) + ((n – 1) * Pn-1) + ((n – 2) * Pn-2) + … ((n – (n – 1)) * Pn – (n-1)) / (n + (n – 1) + … + (n – (n – 1)))
Eksempel:
En 4 bar vægtet glidende gennemsnit med priser på 1,2900, 1,2900, 1,2903 og 1,2904 ville give en glidende gennemsnit på 1,2903 anvendelse af den beregningsmetode ((4 * 1,2904) + (3 * 1,2903) + (2 * 1,2900) + ( 1 * 1,2900)) / (4 + 3 + 2 + 1) = 1,2903
Exponential Moving Average
Denne type glidende gennemsnit reagerer hurtigere på de seneste prisændringer end et simpelt glidende gennemsnit.
Den eksponentielle glidende gennemsnit er et vægtet gennemsnit af de sidste n priser, hvor vægtning aftager eksponentielt med hver tidligere pris.
Beregning:
EMAn-1 + ((2 / (n + 1)) * (Pn – EMAn-1))
Eksempel:
En 4 bar eksponentielt glidende gennemsnit med priser på 1,5554, 1,5555, 1,5558 og 1,5560 ville give en glidende gennemsnit på 1,5558 bruge beregningen 1,5556 + ((2 / (4 + 1)) * (1,5560 til 1,5556)) = 1,5558
Hvilken betydning har længden af Moving Average?
Glidende gennemsnit tillader brugeren frit at vælge, hvilken tidsramme, der skal anvendes. De mest almindelige tidsrum, der anvendes i glidende gennemsnit er 20, 50, 100 og 200 dage. Jo kortere tidshorisont, der anvendes til at skabe den gennemsnitlige, jo mere følsomme vil det være over for prisændringer.
Jo længere tidshorisont, jo mindre følsomme eller mere udglattet, vil gennemsnittet være. Man kan ikke på forhånd sige hvilken tidshorisont der er den rigtige at anvende. Den bedste måde at finde ud af hvilken en der passer bedst til dig er at eksperimentere med en række forskellige tidsperioder, indtil du finder en der passer til din strategi.
Ingen Moving Average er fejlsikker
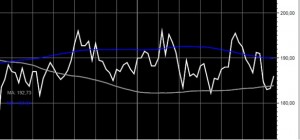
Hvis en aktie bouncer ved support-linjen af det glidende gennemsnit hver eneste gang, så ville vi alle være millardærer. En af de klare ulemper ved at bruge glidende gennemsnit er at de er relativt ubrugelige når aktiekursen bevæger sig sidelæns i forhold når en tydelig trend hersker.
Aktiekursen kan passere gennem et glidende gennemsnit mange gange, hvor udviklingen bevæger sig sidelæns, hvilket gør det vanskeligt at beslutte, hvornår man skal handle. Dette diagram er et godt eksempel på, hvordan den støtte og modstand karakteristika glidende gennemsnit er ikke altid til stede.
Vær opmærksom på forsinkelse
Det er meget vigtigt at forstå, at Moving Average beregnes allerede eksisterende data, dvs. hændelser fra fortiden. Forsinkelsen kan få investorer til at foretage handler hvor det ikke er fordelagtigt.
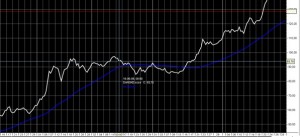
Glidende gennemsnit er indikatorer med historisk data, hvilket betyder, at de ikke kan forudsige nye tendenser. De kan dog godt bekræfte trends, når de er blevet etableret. Som du kan se i diagrammet nedenfor, anses en aktie for at være i en optrend, når prisen er over en glidende gennemsnit og gennemsnittet er skrånende opad. Omvendt vil en investor anvende en lavere aktiekurs end en nedadgående skrå gennemsnit for at bekræfte en nedadgående trend. Mange investorer vil kun overveje at holde en lang position i en aktie, når aktiekursen er handlet over det glidende gennemsnit.
Trend
En aktie anses at være i opadgående trend når Moving Average ligger under aktiekursen samtidig med at Moving Average bevæger sig opad. Det modsatte vil betyde at aktien er i nedadgående trend.
Momentum
Mange spørger, hvordan det er muligt at måle momentum, og hvordan glidende gennemsnit kan bruges til at håndtere en sådan præstation. Det enkle svar er at være meget opmærksom på de tidsfrister, der er defineret til at skabe de forskellige MA, da hver periode kan give værdifuld indsigt i forskellige typer af momentum. Generelt kan momentum ved kortvarige MA måles ved at kigge på glidende gennemsnit, der fokuserer på perioder på 20 dage eller derunder.
Ser man på glidende gennemsnit, der er defineret med en periode på 20 til 100 dage betragtes generelt som en god målestok på mellemlang sigt. Alle glidende gennemsnit, der anvender 100 dage eller mere i beregningen, kan bruges som en målestok for det langsigtede.
En af de bedste metoder til at måle styrke og retning af et værdipapirs momentum er, at placere tre glidende gennemsnit på et diagram og derefter være opmærksomme på hvordan de ligger i forhold til hinanden. De tre mest anvendte definitioner af glidende gennemsnit, har forskellige tidsrammer i et forsøg på at repræsentere korte (50), mellemlange (100) og langsigtede (200) kursudvikling.
Stærk opadgående trend ses, når et glidende gennemsnit med kort tidshorisont ligger over et glidende gennemsnit med længere sigt, og de to gennemsnit er divergerende. Det omvendte gør sig gældende når et gennemsnit med kortere horisont er placeret under et mere langsigtet glidende gennemsnit.
Støtte
Glidende gennemsnits kan også anvendes til at måle et værdipapirs støttepunkt ud fra den historiske kursudvikling. Støttepunkterne anses som potentielle prisstøtter og skal derfor ikke anses som reelle prisstøtter. Det tager ikke lang tid at bemærke, at de faldende kurser på et værdipapir, ofte vil standse og vende retning på samme måde som et vigtigt gennemsnit.
Modstand
Når kursen på et værdipapir falder under et vigtigt støttepunkt, som den 200-dages glidende gennemsnit, er det ikke ualmindeligt at se det glidende gennemsnit fungere som en stærk barriere, der nærmest forhindrer investorer fra at presse prisen tilbage over gennemsnittet.
Mange “short”-investorer vil også bruge disse gennemsnit som indgangspunkter, da prisen ofte springer tilbage fra modstandslinjen og fortsætter med at søge lavere. Investorer der er i besiddelse af en lang position i et værdipapir, bør meget opmærksomme ved handel under store glidende gennemsnit som f.eks. 200-dages gennemsnittet.
StopLoss
Den støtte og modstand analyse glidende gennemsnit tilbyder investorer, gør det til et godt værktøj til risikostyring. Mulighed for at identificere strategiske steder at sætte stop-loss ordrer giver investorer mulighed for at undgå at større tab i sine beholdninger.